Crunching the numbers: Game trees: Difference between revisions
m (just adding some links. Also, no space in ThunderPunch) |
Xan Hutcheon (talk | contribs) No edit summary |
||
| Line 70: | Line 70: | ||
While we humans might not be as efficient as Deep Blue at evaluating these game trees, it should be comforting to know that human chess players are still able to compete against the world’s best chess machines. I’ve always wondered exactly what it was that allowed us to win against the computer. Is it skill? Luck? Experience? Perhaps we too make hundreds of millions of calculations a second, and we don’t even realize it. Either way, it’s a long and tough road to become one of the few who can beat a world class chess computer. But one thing is for certain: those Grand Masters could never have been the best in the world if they gave up. | While we humans might not be as efficient as Deep Blue at evaluating these game trees, it should be comforting to know that human chess players are still able to compete against the world’s best chess machines. I’ve always wondered exactly what it was that allowed us to win against the computer. Is it skill? Luck? Experience? Perhaps we too make hundreds of millions of calculations a second, and we don’t even realize it. Either way, it’s a long and tough road to become one of the few who can beat a world class chess computer. But one thing is for certain: those Grand Masters could never have been the best in the world if they gave up. | ||
{{Crunching}} | |||
Latest revision as of 00:28, 29 May 2012
|
|
If you’re nerd intolerant, you may wish to skip ahead a few paragraphs. Way back in 1996 when I was a wee lass, a technological marvel occurred. For the first time ever, a computer was able to defeat a world champion at a single round of chess. Those interested in the study of AI will quickly recognize this as when IBM’s creation, Deep Blue, defeated Garry Kasparov.
There are a lot of controversies about the fairness of the match, but those aside, there’s still a lot we can learn from Deep Blue and how it plays. A computer scientist friend of mine once described computers to me as really efficient morons, and it may be surprising to know that chess programs are no different.
Computer programs are only as clever as their programmer, and the way they work is by following a set of instructions that are laid out for them. This can be really challenging since computers don’t speak and listen in the same sense we do, so programmers transcribe their instructions into a language the computer can understand. Java, C++, and Python are examples of the languages a computer can comprehend. Chess computers compete by looking at all possible moves it can make.
For example, if the computer was white and was the player to move, it has three choices: move the king up, diagonally up and right, or right. Next, it looks at all the possible moves its opponent could make. Black could move his/her/its pawn down, the king down, down-left, or left. Then the computer looks at each move it could make after that, and then each move the opponent could make after that, and so on and so on and so on until it runs out of time. Finally, it looks at all the possible combinations of moves that it predicted and will choose a move which will give it a better chance at being ahead later in the game. This may seem like an inefficient way to play, especially at the beginning of a game when there are more pieces, but chess computers are very quick. Within one second, Deep Blue evaluated two hundred million positions.
Let’s apply Deep Blue’s strategy to our favorite game, Pokémon. Let’s say your friend and you are arguing once more about what movie you guys should watch. Since you mopped the floor with your friend last time (metaphorically, of course), you let your friend decide on the condition of the match. Your friend has gotten into breeding recently and comes to the conclusion you should each pick one level 1 Pokémon with no hold items and duke them out.
Your opponent chooses an Elekid who knows Rain Dance (1), Thunderbolt (2), Ice Punch (3), and Psychic (4). You decide to go with your bff, Magby, with Belly Drum (1), Mach Punch (2), Fire Punch (3) and ThunderPunch (4). Both of these Pokémon have their Hidden Ability Inner Focus.
The Pokémon’s stats are set ups as follows.
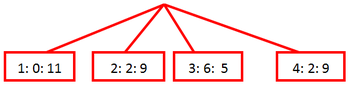
Now it’s time to hop into the WABAC machine and think back to when we talked about graph theory. We’re going to use a special type of graph called a game tree. Game trees are used to help us visualize what could happen based on the current position of a game. For the sake of simplicity, we’re going to use the average damage an attack will have. Since Elekid is slower than Magby, the top of the tree will look like this:
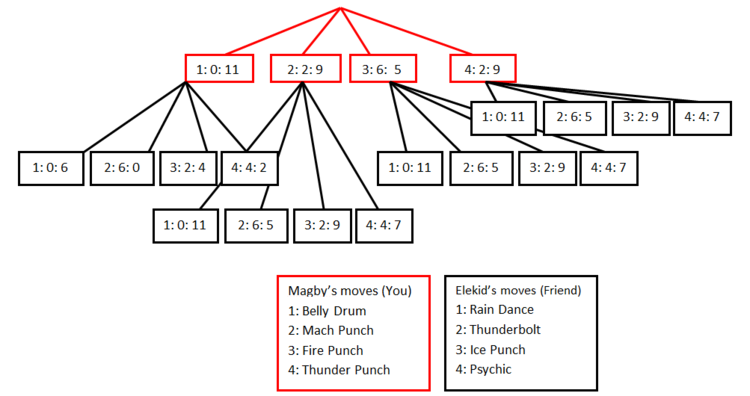
Here, we’re representing your possible moves with red, and the numbers inside the boxes read Move Number: Damage Dealt: Opponent’s Remaining Health. So 1: 0: 11 means that Magby used Belly Drum, it didn’t do any damage, and Elekid has 11 health left. However, if Magby used Belly Drum, the next time it attacks, it will do way more damage, but it will also lose 5 HP. Next, we’ll look at all the possible moves Elekid can make from here.
Here, we represent Elekid’s possible moves with black. It’s only been one turn, and this graph is already getting pretty complicated, so we’re going to use a skill that can make human players better than computers: heuristics. This is a fancy word for eliminating branches of the game tree because we believe that other branches are just better. For example, if we were to write this first turn as a game theory table, we would quickly see that Elekid’s Thunderbolt is always better than its Psychic or Ice Punch:
We also see that Magby’s Fire Punch is always just better than its Mach Punch (especially since it’s faster than Elekid anyway) and ThunderPunch. However, this technique can also be pretty dangerous. Belly Drum and Rain Dance do not have immediate benefits, so if we were only playing for one turn, we could discount them. However, since we’re playing until a knock out, we can’t just throw these branches away. This is where experience as a player really comes in handy. Looking at how this game is set up where there is nothing else to switch into and no one is holding anything, we can be confident in eliminating Pyschic, Ice Punch, Mach Punch, and ThunderPunch since they will always be outclassed.
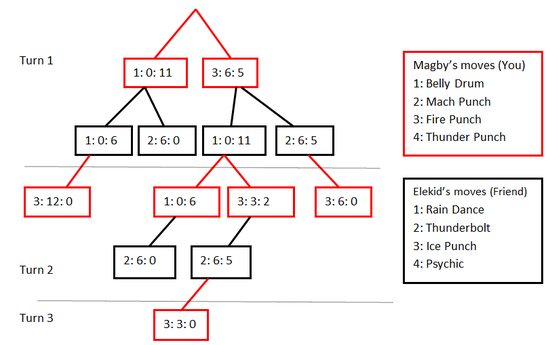
This makes our graph much less intimidating, and when we take it out to game completion, it will look like this:
When we look at the ends of the tree, we can see three ways for you to win (the red ends), and two ways for your opponent to win (the black ends). Unfortunately, the more ways for a player to win doesn’t necessarily mean that the player is more likely to win. Some strategies are fairly risky.
Suppose, for example, if you were to use Belly Drum on your first turn. This relates to the left part of the graph. You might get greedy and see the chance to deal 12 damage in one blow. You’d be knocking them out in one hit! But if your opponent ever had a hint that this was the move you were going to play, than your friend would choose to use Thunderbolt, taking advantage of your now lower health and stealing your victory.
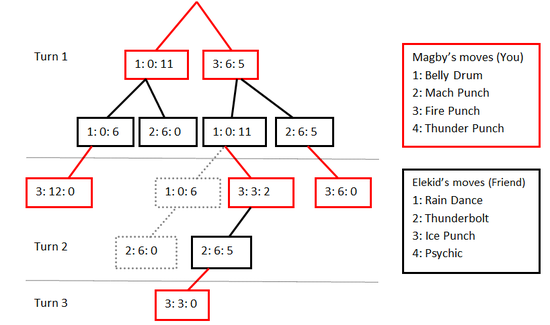
Like with our game theory table, the trick is to pick the move that will minimize the damage you take and maximize the damage you deal. So how do we do that? By working backwards! Look at each time a player makes a choice. In our game, there are only four: you’re turn at the beginning of the game, the two choices your opponent can make after your first choice, and the choice you can make in turn two. Whenever a player makes a choice, he or she wants pick the move that will make them win. We’re going to look at the ends of the tree, and prune the branches that won’t be in the decider’s favor.
The closest choice towards the end of the tree is yours in Turn 2. If we go with Belly Drum, we will ultimately loose due to the sacrifice to HP, so we’ll go with the winning choice of Fire Punch. We’ll represent deleted choices with a dashed line.
Next we’ll look at the choice your opponent can make during the first turn. This is a bit trickier since when this decision is made, your friend can’t tell for sure what your first move will be. However, since we’ve eliminated one way for Elekid to win, the only other way is if you use Belly Drum and your opponent uses Thunderbolt on the first turn. So all you have to do is repeatedly use Fire Punch and you’ll win. That being said, your opponent would still probably choose Thunderbolt in case you made a mistake.
While we humans might not be as efficient as Deep Blue at evaluating these game trees, it should be comforting to know that human chess players are still able to compete against the world’s best chess machines. I’ve always wondered exactly what it was that allowed us to win against the computer. Is it skill? Luck? Experience? Perhaps we too make hundreds of millions of calculations a second, and we don’t even realize it. Either way, it’s a long and tough road to become one of the few who can beat a world class chess computer. But one thing is for certain: those Grand Masters could never have been the best in the world if they gave up.
| Crunching the Numbers |
|---|
| By Danielle Detering |
| Crunching the numbers • Graph theory • Game theory Game trees • Mixed strategies |