Crunching the numbers: Game theory
|
|
With Pokémon, as with a plethora of other games, one of the key ingredients for winning a battle is the ability to predict your opponent. Unfortunately, since the majority of us do not have telepathic mind powers, this can be a difficult task. It is due to the complex nature of prediction that mathematicians developed a theory on how people play games. We cleverly call this "Game Theory."
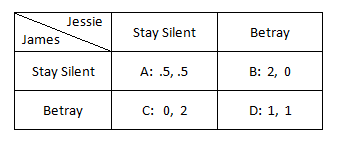
Let’s start out with a simple, one turn, two-player game. Let’s say Officer Jenny catches Jessie and James. Much to her dismay, she wasn’t able to catch them red handed, so decides to set up a little experiment to see if she can get them to confess. After separating the rocket duo, she gives them both the same spiel. If one criminal stays silent while the other admits that his or her partner committed a crime, then the betrayer goes free and the silent one gets two years of jail time. If they are both silent, then they are dealt only a half a year sentence for minor charges. However, if they both betray the other, than they both receive a year of jail time. Game Theorists have a special name for this scenario. They call this "The Prisoner’s Dilemma." To make it easier to study the situation, we set up a matrix like this.
Here, Jessie’s potential actions are listed in the top row and they are compared to James’ potential actions listed in the left column. The possible outcomes are listed in the cells A,B, C, and D. In these cells, the numbers on the left are James’ possible jail time, and the numbers on the right are Jessie’s possible jail time. In B, Jessie gets zero years of jail time for betraying James when he is silent, and thus earns him two years of jail time. This is vice-versa in cell C.
An optimist might believe that the rocket duo would both decide to stay silent since the rewards for cell A, if added up, is less jail time than those in other cells. This is not the case. Let’s look at the rewards for being silent versus betraying. If James stays silent when Jessie is silent, he gets .5 years of prison, but he would end up with zero years if he betrays. Now if James is silent when Jessie betrays, he gets two years as compared to only one year if he betrays. Therefore, no matter what Jessie decides to pick it is best for James to betray. Since Jessie is faced with the same situation, it is also in her best interest to betray. Conclusively, since they decided to betray each other, the result is D: they both get one year of prison.
Now some readers may be thinking, "Woah, woah, woah, wait a second. Jessie would never betray James, and James would never betray Jessie." It’s true, there could be outside influences that this model does not account for. Game Theory only works when the players are driven to optimize their rewards and win. In the real world, as players in tournaments are usually motivated to win, Game Theory is an excellent model for the decision process of competitors.
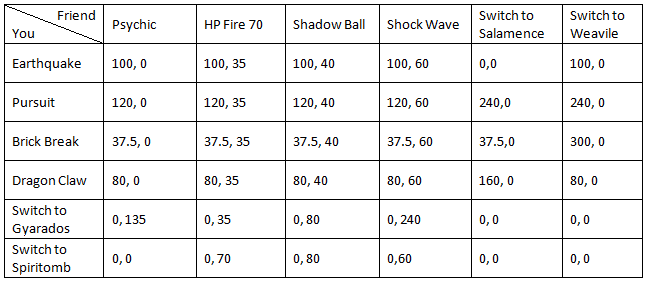
Let’s say you and a friend are arguing over what movie you should watch tonight, so each of you whip out your DSes and decide to battle to see who picks the flick. You gotta win. Your friend is horrible at picking movies, and you don’t want to sit for two hours watching something boring. The stakes are high. It's turn one, and you throw out a super beastly Tyranitar with Earthquake, Pursuit, Brick Break, and Dragon Claw. Your friend throws out an Alakazam. You know from experience that this Alakazam has Psychic, Hidden Power (Fire 70), Shadow Ball, and Shock Wave. The other Pokémon on your team are Gyarados and Spiritomb. The other Pokémon on your opponent’s team are Salamence and Weavile. Setting up a matrix of base powers (STAB, Pursuit’s effect on switching, weaknesses and resistances included) to represent this turn we get:
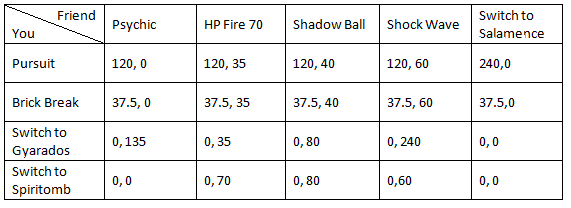
In this case, not only are we trying to maximize our potential damage, but we’re also trying to minimize the damage your opponent will inflict. A six by six game looks a lot scarier, but since some moves are just flat-out better than others, we can ignore them. For starters, Pursuit is simply better than Earthquake or Dragon Claw. We can remove Earthquake and Dragon Claw from our matrix which results in a four by six game.
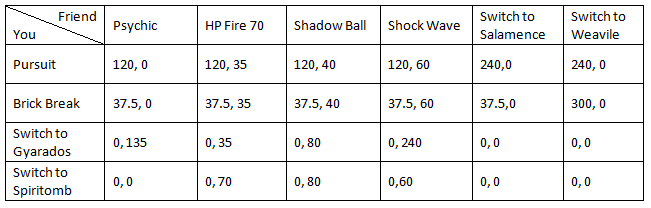
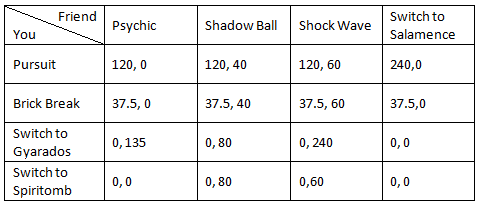
See? This matrix is getting less scary already. Of course, if your opponent is able to figure out your optimal moves, then it helps determine his or her optimal moves. For instance, in our original six by six game, whether or not it was better to switch in with Salamence or Weavile depended on if you used Earthquake, Brick Break, or Dragon Claw. Since we removed Earthquake and Dragon Claw, Salamence outclasses Weavile.
Your opponent would also make a better choice using Shadow Ball over Hidden Power Fire 70.
In this four by four game, Pursuit outclasses all of your other choices.
Now that we know that the best attack for you to use is Pursuit, there’s only good move your opponent can use to best retaliate: Shock Wave.
Seeing how not only are you dishing out the higher base power, but you're also dealing immense physical damage to a special glass cannon, it looks like you’re one step closer to picking the movie for the evening. Naturally, using attacks with the highest base power isn’t the only way to win Pokémon. Using Pokémon with proper base stats, correctly choosing special or physical moves, deciding to use a stat enhancing or status inflicting move at the right time are all key parts to being victorious. Game theory does account for games with multiple turns, but that is a different discussion for a different day.
| Crunching the Numbers |
|---|
| By Danielle Detering |
| Crunching the numbers • Graph theory • Game theory Game trees • Mixed strategies |